【PyTorch】ニューラルネットワークを構築する方法【NN】
今回は、PyTorch を使って、ニューラルネットワーク(NN)を構築したときのメモです。
ファッションアイテムの公開データセットである Fashion-MNIST を用いて、ニューラルネットワークを構築し、学習・テストまでを行います。
Fashion-MNIST については、以前の記事にまとめてありますので、もしよければ参考にしてみてください。
【Fashion-MNIST】ファッションアイテムのデータセットを使ってみた【TensorFlow】
動作環境としては、Anaconda の jupyter 上で動かし、CPU の AMD Ryzen 7 を使っています。
Contents
データセットの読み込み
まず、データセットのダウンロードと読み込みを行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
''' 1. データの読み込みと前処理 ''' from torchvision import datasets import torchvision.transforms as transforms from torch.utils.data import DataLoader # ダウンロード先のディレクトリ root = './data' # Transformオブジェクトを生成 transform = transforms.Compose( [transforms.ToTensor(), # Tensorオブジェクトに変換 transforms.Normalize((0.5), (0.5)), # 平均0.5、標準偏差0.5で正規化 lambda x: x.view(-1), # データの形状を(28,28)から(784,)に変換 ]) # 訓練用データの読み込み(60000セット) f_mnist_train = datasets.FashionMNIST( root=root, # データの保存先のディレクトリ download=True, # ダウンロードを許可 train=True, # 訓練データを指定 transform=transform) # トランスフォーマーオブジェクトを指定 # テスト用データの読み込み(10000セット) f_mnist_test = datasets.FashionMNIST( root=root, # データの保存先のディレクトリ download=True, # ダウンロードを許可 train=False, # テストデータを指定 transform=transform) # トランスフォーマーオブジェクトを指定 # ミニバッチのサイズ batch_size = 64 # 訓練用のデータローダー train_dataloader = DataLoader(f_mnist_train, # 訓練データ batch_size=batch_size, # ミニバッチのサイズ shuffle=True) # シャッフルして抽出 # テスト用のデータローダー test_dataloader = DataLoader(f_mnist_test, # テストデータ batch_size=batch_size, # ミニバッチのサイズ shuffle=False) # シャッフルして抽出 # データローダーが返すミニバッチの先頭データの形状を出力 for (x, t) in train_dataloader: # 訓練データ print(x.shape) print(t.shape) break for (x, t) in test_dataloader: # テストデータ print(x.shape) print(t.shape) break |
以下のように、「data」フォルダが作成され、データセットがダウンロードされます。
jupyter 上での出力は以下のようになりました。
ニューラルネットワーク(NN)の入力は、畳込みニューラルネットワークと違って、フラットな形状である必要があるため、
「lambda x: x.view(-1)」として、2階テンソルを1階テンソルに変換しています。
「lambda」は、「lambda 引数: 返り値」というように定義して使います。
また、「batch_size = 64」として、ミニバッチのサイズを 64 としています。
ミニバッチは、1回の学習・テストに用いるデータの数を指定しています。データはランダムに抽出して使います。
最後の出力は以下のようになり、訓練データ・テストデータのミニバッチのサイズが確認できます。
|
1 2 3 4 |
torch.Size([64, 784]) torch.Size([64]) torch.Size([64, 784]) torch.Size([64] |
ニューラルネットワークのモデルを定義・生成
モデルの定義、生成を行い、その構造を出力します。今回は、2層の浅いネットワークとなっています。
モデルの定義は、以下のように行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
''' 2. モデルの定義 ''' import torch import torch.nn as nn class MLP(nn.Module): '''多層パーセプトロン Attributes: l1(Linear) : 隠れ層 l2(Linear) : 出力層 d1(Dropout): ドロップアウト ''' def __init__(self, input_dim, hidden_dim, output_dim): '''モデルの初期化を行う Parameters: input_dim(int) : 入力する1データあたりの値の形状 hidden_dim(int): 隠れ層のユニット数 output_dim(int): 出力層のユニット数 ''' # スーパークラスの__init__()を実行 super().__init__() # 隠れ層 self.fc1 = nn.Linear(input_dim, # 入力するデータのサイズ hidden_dim) # 隠れ層のニューロン数 # ドロップアウト self.d1 = nn.Dropout(0.5) # 出力層 self.fc2 = nn.Linear(hidden_dim, # 入力するデータのサイズ # (=前層のニューロン数) output_dim) # 出力層のニューロン数 def forward(self, x): '''MLPの順伝播処理を行う Parameters: x(ndarray(float32)):訓練データ、または検証データ Returns(float32): 出力層からの出力値 ''' # レイヤー、活性化関数に前ユニットからの出力を入力する x = self.fc1(x) x = torch.sigmoid(x) x = self.d1(x) x = self.fc2(x) # 最終出力は活性化関数を適用しない return x |
ここではモデルを定義しているだけなので、出力はありません。
次にモデルの生成を行います。
モデルの生成は、以下のように行います。
|
1 2 3 4 5 6 7 8 9 10 11 |
''' 3. モデルの生成 ''' # 使用可能なデバイス(CPUまたはGPU)を取得する device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') print(torch.cuda.is_available()) # モデルオブジェクトを生成し、使用可能なデバイスを設定する model = MLP(784, 256, 10).to(device) model # モデルの構造を出力 |
「torch.cuda.is_available()」で GPU が使用可能か確認することができます。「True」が返れば、GPU が使えるということになります。
モデルの構造は、以下のようになりました。
|
1 2 3 4 5 |
MLP( (fc1): Linear(in_features=784, out_features=256, bias=True) (d1): Dropout(p=0.5, inplace=False) (fc2): Linear(in_features=256, out_features=10, bias=True) ) |
「out_features=10」は、 Fashion-MNIST が10種類あるため、10種類のファッションアイテムを分類するためです。
損失関数と最適化手法の設定
損失関数と最適化手法(オプティマイザー)の設定を行います。
最適化手法には、勾配降下アルゴリズムを用います。
|
1 2 3 4 5 6 7 8 9 |
''' 4. 損失関数とオプティマイザーの生成 ''' import torch.optim # クロスエントロピー誤差のオブジェクトを生成 criterion = nn.CrossEntropyLoss() # 勾配降下アルゴリズムを使用するオプティマイザーを生成 optimizer = torch.optim.SGD(model.parameters(), lr=0.1) |
パラメータ更新用の関数を定義
学習時のパラメータを更新する train_step 関数を定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
''' 5. train_step()関数の定義 ''' def train_step(x, t): '''バックプロパゲーションによるパラメーター更新を行う Parameters: x: 訓練データ t: 正解ラベル Returns: MLPの出力と正解ラベルのクロスエントロピー誤差 ''' model.train() # モデルを訓練(学習)モードにする preds = model(x) # モデルの出力を取得 loss = criterion(preds, t) # 出力と正解ラベルの誤差から損失を取得 optimizer.zero_grad() # 勾配を0で初期化(累積してしまうため) loss.backward() # 逆伝播の処理(自動微分による勾配計算) optimizer.step() # 勾配降下法の更新式を適用してバイアス、重みを更新 return loss, preds |
モデル評価用の関数を定義
テストデータを使って評価を行うための test_step 関数を定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
''' 6. test_step()関数の定義 ''' def test_step(x, t): '''テストデータを入力して損失と予測値を返す Parameters: x: テストデータ t: 正解ラベル Returns: MLPの出力と正解ラベルのクロスエントロピー誤差 ''' model.eval() # モデルを評価モードにする preds = model(x) # モデルの出力を取得 loss = criterion(preds, t) # 出力と正解ラベルの誤差から損失を取得 return loss, preds |
早期終了判定を行う関数を定義
早期終了判定を行う EarlyStopping 関数を定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
''' 7. 学習の進捗を監視し早期終了判定を行うクラス ''' class EarlyStopping: def __init__(self, patience=10, verbose=0): ''' Parameters: patience(int): 監視するエポック数(デフォルトは10) verbose(int): 早期終了の出力フラグ 出力(1),出力しない(0) ''' # インスタンス変数の初期化 # 監視中のエポック数のカウンターを初期化 self.epoch = 0 # 比較対象の損失を無限大'inf'で初期化 self.pre_loss = float('inf') # 監視対象のエポック数をパラメーターで初期化 self.patience = patience # 早期終了メッセージの出力フラグをパラメーターで初期化 self.verbose = verbose def __call__(self, current_loss): ''' Parameters: current_loss(float): 1エポック終了後の検証データの損失 Return: True:監視回数の上限までに前エポックの損失を超えた場合 False:監視回数の上限までに前エポックの損失を超えない場合 ''' # 前エポックの損失より大きくなった場合 if self.pre_loss < current_loss: self.epoch += 1 # カウンターを1増やす # 監視回数の上限に達した場合 if self.epoch > self.patience: if self.verbose: # 早期終了のフラグが1の場合 print('early stopping') # メッセージを出力 return True # 学習を終了するTrueを返す # 前エポックの損失以下の場合 else: self.epoch = 0 # カウンターを0に戻す self.pre_loss = current_loss # 損失の値を更新する # 監視回数の上限までに前エポックの損失を超えなければ # Falseを返して学習を続行する # 前エポックの損失を上回るが監視回数の範囲内であれば # Falseを返す必要があるので、return文の位置はここであることに注意 return False |
学習
実際に、学習・テストを繰り返し行います。
エポック数が 200 に設定されているため、最大200回繰り返されます。
「%%time」とすることで実行時間を計測することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
%%time ''' 8.モデルを使用して学習する ''' from sklearn.metrics import accuracy_score # エポック数 epochs = 200 # 損失と精度の履歴を保存するためのdictオブジェクト history = {'loss':[],'accuracy':[], 'test_loss':[], 'test_accuracy':[]} # 早期終了の判定を行うオブジェクトを生成 ers = EarlyStopping(patience=5, # 監視対象回数 verbose=1) # 早期終了時にメッセージを出力 # 学習を行う for epoch in range(epochs): train_loss = 0. # 訓練1エポックあたりの損失を保持する変数 train_acc = 0. # 訓練1エポックごとの精度を保持する変数 test_loss = 0. # 評価1エポックごとの損失を保持する変数 test_acc = 0. # 評価1エポックごとの精度を保持する変数 # 1ステップにおける訓練用ミニバッチを使用した学習 for (x, t) in train_dataloader: # torch.Tensorオブジェクトにデバイスを割り当てる x, t = x.to(device), t.to(device) loss, preds = train_step(x, t) # 損失と予測値を取得 train_loss += loss.item() # ステップごとの損失を加算 train_acc += accuracy_score( t.tolist(), preds.argmax(dim=-1).tolist() ) # ステップごとの精度を加算 # 1ステップにおけるテストデータのミニバッチを使用した評価 for (x, t) in test_dataloader: # torch.Tensorオブジェクトにデバイスを割り当てる x, t = x.to(device), t.to(device) loss, preds = test_step(x, t) # 損失と予測値を取得 test_loss += loss.item() # ステップごとの損失を加算 test_acc += accuracy_score( t.tolist(), preds.argmax(dim=-1).tolist() ) # ステップごとの精度を加算 # 訓練時の損失の平均値を取得 avg_train_loss = train_loss / len(train_dataloader) # 訓練時の精度の平均値を取得 avg_train_acc = train_acc / len(train_dataloader) # 検証時の損失の平均値を取得 avg_test_loss = test_loss / len(test_dataloader) # 検証時の精度の平均値を取得 avg_test_acc = test_acc / len(test_dataloader) # 訓練データの履歴を保存する history['loss'].append(avg_train_loss) history['accuracy'].append(avg_train_acc) # テストデータの履歴を保存する history['test_loss'].append(avg_test_loss) history['test_accuracy'].append(avg_test_acc) # 1エポックごとに結果を出力 if (epoch + 1) % 1 == 0: print( 'epoch({}) train_loss: {:.4} train_acc: {:.4} val_loss: {:.4} val_acc: {:.4}'.format( epoch+1, avg_train_loss, # 訓練データの損失を出力 avg_train_acc, # 訓練データの精度を出力 avg_test_loss, # テストデータの損失を出力 avg_test_acc # テストデータの精度を出力 )) # 検証データの損失をEarlyStoppingオブジェクトに渡して早期終了を判定 if ers(avg_test_loss): # 監視対象のエポックで損失が改善されなければ学習を終了 break |
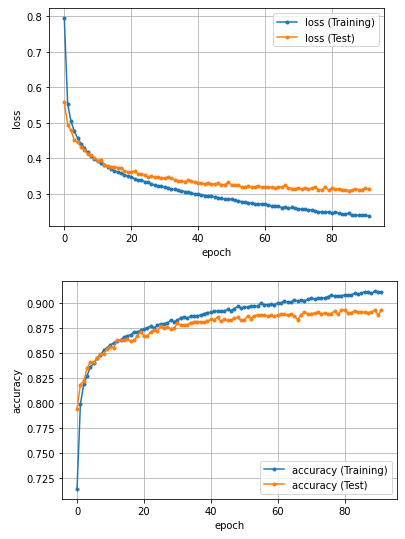
結果、73エポックで終了となりました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
epoch(1) train_loss: 0.5519 train_acc: 0.8 val_loss: 0.4955 val_acc: 0.8206 epoch(2) train_loss: 0.5046 train_acc: 0.8181 val_loss: 0.4672 val_acc: 0.8287 epoch(3) train_loss: 0.4743 train_acc: 0.8285 val_loss: 0.4498 val_acc: 0.8356 epoch(4) train_loss: 0.4547 train_acc: 0.8363 val_loss: 0.4333 val_acc: 0.8427 epoch(5) train_loss: 0.4383 train_acc: 0.8422 val_loss: 0.4259 val_acc: 0.844 epoch(6) train_loss: 0.4277 train_acc: 0.8452 val_loss: 0.4257 val_acc: 0.8471 epoch(7) train_loss: 0.4138 train_acc: 0.8513 val_loss: 0.4126 val_acc: 0.8488 epoch(8) train_loss: 0.4063 train_acc: 0.8524 val_loss: 0.4013 val_acc: 0.8541 epoch(9) train_loss: 0.3997 train_acc: 0.8557 val_loss: 0.4034 val_acc: 0.8516 epoch(10) train_loss: 0.3942 train_acc: 0.8568 val_loss: 0.3882 val_acc: 0.8586 epoch(11) train_loss: 0.3869 train_acc: 0.8588 val_loss: 0.3842 val_acc: 0.8611 epoch(12) train_loss: 0.3801 train_acc: 0.8626 val_loss: 0.3818 val_acc: 0.8621 epoch(13) train_loss: 0.3729 train_acc: 0.8648 val_loss: 0.3822 val_acc: 0.8598 epoch(14) train_loss: 0.3677 train_acc: 0.8674 val_loss: 0.3765 val_acc: 0.8649 epoch(15) train_loss: 0.3663 train_acc: 0.8682 val_loss: 0.3744 val_acc: 0.8678 epoch(16) train_loss: 0.361 train_acc: 0.8686 val_loss: 0.3691 val_acc: 0.8682 epoch(17) train_loss: 0.3574 train_acc: 0.8696 val_loss: 0.3665 val_acc: 0.8698 epoch(18) train_loss: 0.3535 train_acc: 0.8713 val_loss: 0.3616 val_acc: 0.871 epoch(19) train_loss: 0.3512 train_acc: 0.8728 val_loss: 0.3614 val_acc: 0.8715 epoch(20) train_loss: 0.3475 train_acc: 0.8726 val_loss: 0.3568 val_acc: 0.8708 epoch(21) train_loss: 0.3445 train_acc: 0.8755 val_loss: 0.3564 val_acc: 0.8736 epoch(22) train_loss: 0.3403 train_acc: 0.8756 val_loss: 0.3583 val_acc: 0.8737 epoch(23) train_loss: 0.3356 train_acc: 0.8774 val_loss: 0.3534 val_acc: 0.8734 epoch(24) train_loss: 0.3334 train_acc: 0.8774 val_loss: 0.3491 val_acc: 0.8762 epoch(25) train_loss: 0.3317 train_acc: 0.8794 val_loss: 0.3491 val_acc: 0.8759 epoch(26) train_loss: 0.3291 train_acc: 0.8807 val_loss: 0.3522 val_acc: 0.8768 epoch(27) train_loss: 0.3269 train_acc: 0.8811 val_loss: 0.3471 val_acc: 0.8775 epoch(28) train_loss: 0.3239 train_acc: 0.881 val_loss: 0.3481 val_acc: 0.8749 epoch(29) train_loss: 0.3214 train_acc: 0.8815 val_loss: 0.3442 val_acc: 0.8771 epoch(30) train_loss: 0.318 train_acc: 0.884 val_loss: 0.3394 val_acc: 0.8809 epoch(31) train_loss: 0.3153 train_acc: 0.8842 val_loss: 0.3403 val_acc: 0.8799 epoch(32) train_loss: 0.3156 train_acc: 0.8847 val_loss: 0.3396 val_acc: 0.88 epoch(33) train_loss: 0.3127 train_acc: 0.8855 val_loss: 0.341 val_acc: 0.8769 epoch(34) train_loss: 0.3099 train_acc: 0.8855 val_loss: 0.3435 val_acc: 0.876 epoch(35) train_loss: 0.3073 train_acc: 0.887 val_loss: 0.3405 val_acc: 0.8732 epoch(36) train_loss: 0.306 train_acc: 0.8881 val_loss: 0.3355 val_acc: 0.8804 epoch(37) train_loss: 0.3045 train_acc: 0.8879 val_loss: 0.335 val_acc: 0.8821 epoch(38) train_loss: 0.3031 train_acc: 0.8902 val_loss: 0.3318 val_acc: 0.8834 epoch(39) train_loss: 0.3003 train_acc: 0.89 val_loss: 0.3327 val_acc: 0.8833 epoch(40) train_loss: 0.2998 train_acc: 0.8905 val_loss: 0.3346 val_acc: 0.8824 epoch(41) train_loss: 0.2988 train_acc: 0.8901 val_loss: 0.3284 val_acc: 0.8837 epoch(42) train_loss: 0.2963 train_acc: 0.8914 val_loss: 0.3335 val_acc: 0.8796 epoch(43) train_loss: 0.2922 train_acc: 0.8928 val_loss: 0.3337 val_acc: 0.8851 epoch(44) train_loss: 0.2924 train_acc: 0.892 val_loss: 0.3308 val_acc: 0.8822 epoch(45) train_loss: 0.2891 train_acc: 0.8939 val_loss: 0.3259 val_acc: 0.8832 epoch(46) train_loss: 0.2889 train_acc: 0.8934 val_loss: 0.3259 val_acc: 0.8855 epoch(47) train_loss: 0.2872 train_acc: 0.8946 val_loss: 0.3281 val_acc: 0.8839 epoch(48) train_loss: 0.2857 train_acc: 0.8942 val_loss: 0.3242 val_acc: 0.8847 epoch(49) train_loss: 0.2843 train_acc: 0.8956 val_loss: 0.3249 val_acc: 0.8838 epoch(50) train_loss: 0.2831 train_acc: 0.8952 val_loss: 0.3246 val_acc: 0.8865 epoch(51) train_loss: 0.2802 train_acc: 0.8953 val_loss: 0.3229 val_acc: 0.8868 epoch(52) train_loss: 0.2802 train_acc: 0.8969 val_loss: 0.3201 val_acc: 0.8863 epoch(53) train_loss: 0.2783 train_acc: 0.8981 val_loss: 0.3263 val_acc: 0.8859 epoch(54) train_loss: 0.2772 train_acc: 0.8987 val_loss: 0.3221 val_acc: 0.886 epoch(55) train_loss: 0.2758 train_acc: 0.8972 val_loss: 0.3225 val_acc: 0.8843 epoch(56) train_loss: 0.2752 train_acc: 0.899 val_loss: 0.3192 val_acc: 0.8897 epoch(57) train_loss: 0.2741 train_acc: 0.8992 val_loss: 0.3204 val_acc: 0.8872 epoch(58) train_loss: 0.2727 train_acc: 0.8992 val_loss: 0.3273 val_acc: 0.883 epoch(59) train_loss: 0.2713 train_acc: 0.8988 val_loss: 0.3188 val_acc: 0.8857 epoch(60) train_loss: 0.2702 train_acc: 0.9006 val_loss: 0.321 val_acc: 0.8856 epoch(61) train_loss: 0.2686 train_acc: 0.9006 val_loss: 0.3251 val_acc: 0.8868 epoch(62) train_loss: 0.2665 train_acc: 0.9012 val_loss: 0.3212 val_acc: 0.8874 epoch(63) train_loss: 0.2658 train_acc: 0.9019 val_loss: 0.3171 val_acc: 0.8884 epoch(64) train_loss: 0.2648 train_acc: 0.9015 val_loss: 0.3181 val_acc: 0.8885 epoch(65) train_loss: 0.2648 train_acc: 0.9006 val_loss: 0.3186 val_acc: 0.8871 epoch(66) train_loss: 0.2619 train_acc: 0.9029 val_loss: 0.3166 val_acc: 0.8885 epoch(67) train_loss: 0.2622 train_acc: 0.9027 val_loss: 0.3159 val_acc: 0.8894 epoch(68) train_loss: 0.2601 train_acc: 0.9033 val_loss: 0.3165 val_acc: 0.8888 epoch(69) train_loss: 0.2607 train_acc: 0.9032 val_loss: 0.3186 val_acc: 0.8874 epoch(70) train_loss: 0.2597 train_acc: 0.904 val_loss: 0.3194 val_acc: 0.8854 epoch(71) train_loss: 0.2566 train_acc: 0.9053 val_loss: 0.3172 val_acc: 0.89 epoch(72) train_loss: 0.2567 train_acc: 0.9057 val_loss: 0.3159 val_acc: 0.8876 epoch(73) train_loss: 0.2543 train_acc: 0.9049 val_loss: 0.3164 val_acc: 0.8899 early stopping |
CPU での実行時間は約13分でした。
|
1 |
Wall time: 13min 4s |
ちなみに、算出している精度 accuracy は、正解率となります。
精度のグラフ化
エポックごとの損失と精度をグラフ化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
''' 9. 損失と精度の推移をグラフにする ''' import matplotlib.pyplot as plt %matplotlib inline # 損失 plt.plot(history['loss'], marker='.', label='loss (Training)') plt.plot(history['test_loss'], marker='.', label='loss (Test)') plt.legend(loc='best') plt.grid() plt.xlabel('epoch') plt.ylabel('loss') plt.show() # 精度 plt.plot(history['accuracy'], marker='.', label='accuracy (Training)') plt.plot(history['test_accuracy'], marker='.', label='accuracy (Test)') plt.legend(loc='best') plt.grid() plt.xlabel('epoch') plt.ylabel('accuracy') plt.show() |
※横軸の epoc が80を超えていますが、これは一度学習・検証をし直したためです。
参考文献
関連記事
-

-
【Chainer】手書き数字認識をしてみた【Deep Learning】
Chainerを用いて、ニューラルネットワークを構築し、手書き数字認識を行ったときのメモです。
-

-
【探索】縦型・横型・反復深化法の探索手法の比較。
探索とは、チェスや将棋や囲碁などのゲームをコンピュータがプレイするときに、どの手を指すかを決定するの
-

-
【機械学習】 scikit-learn で精度・再現率・F値を算出する方法【Python】
今回は、2クラス分類で Python の scikit-learn を使った評価指標である、精度(P
-

-
【Weka】ARFF 形式から CSV 形式に簡単に変換する方法。
フリーのデータマイニングツールである WEKA では、ARFF 形式と CSV 形式のデータを読み込
-

-
【Weka】CSVファイルを読み込んで決定木を実行。
フリーの機械学習ソフト Weka を使って、CSVファイルを読み込んで決定木(Decision Tr
-

-
【Weka】アソシエーション・ルール(association rule)【機械学習】
フリーの機械学習ツール Weka でアソシエーション・ルール(association rule)を使
-

-
【PyTorch】GPUのメモリ不足でエラーになったときの対処方法。
PyTorch で深層学習していて、 GPUのメモリ不足でエラーが出てしまったので、対処方法のメモで
-

-
【Fashion-MNIST】ファッションアイテムのデータセットを使ってみた【TensorFlow】
今回は、機械学習用に公開されているデータセットの1つである「Fashion-MNIST」について紹介
-

-
【探索】ダイクストラ法・最良優先探索・Aアルゴリズムの比較。
縦型探索や横型探索では、機械的に順序を付け、最小ステップでゴールを目指します。 つまり、
-

-
機械学習の手法のまとめ。
機械学習は、「与えられた入出力事例をモデル化する行為」のことで、ディープラーニングなどで注目を集めて